Physical Property
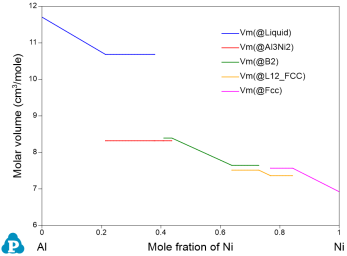
Physical property calculation implemented in Pandat™ allows user to calculate the molar weight, molar volume, density, surface tension and viscosity. The interface is similar to the Thermodynamic property calculation as shown in Figure 1. User can set up the calculation condition as a line calculation and select the properties to be calculated. The default graph is the calculated property as shown in Figure 2 as an example. Again, if two or more properties are selected, all of them will be plotted one by one.
The detailed calculation method for each property and the format of the database file are described in the following sections.
Weight
The molar weight for a phase is calculated from the atomic weights of the elements involved in the phase. The unit is kg/mol·atoms. Since atomic weights of elements have been included in Pandat™, no input is required in the database TDB file.
For example, an Fcc phase in Al-Cu binary system with xAl = 0:9 and xCu = 0:1, its molecular weight is
|
|
(1) |
Volume
The molar volume can be calculated by Pandat™ if the model parameters are properly defined in the database file. The molar volume of a pure component is described as a function of temperature and pressure, and the excess molar volume of a phase is described in the format similar to that of excess Gibbs energy. The unit of molar volume is m3/mol·atoms. In the database (.TDB) file, the format of molar volume is:
PARAMETER Vm(Fcc,Al;0) 298.15 +9.7743e-006
*exp(6.91213e-005*T+1.62267e-011*T**3+0.413484*T**(-1)); 3000 N !
PARAMETER Vm(Fcc,Fe;0) 298.15 +6.72092e-006*exp(6.97895e-005*T); 3000 N !
PARAMETER Vm(Fcc,Al,Fe:Va;0) 298.15 -3e-6; 3000 N !
The calculation of molar volume for a phase is
|
|
(2) |
where is the parameter for the excess molar volume of this phase.
Molar volume of a system with phase mixture is calculated by
|
|
(3) |
where and
are the molar fraction and molar volume for phase
.
Note that, if a phase is described by a compound-energy-formalism (CEF) with multi-sublattices, the molar volume is automatically described as a function of T, P, and site fraction (y) following the format of the Gibbs energy. This will introduce many end members in the molar volume and may lead to instability in the calculated molar volume. In reality, molar volume should be a function of mole fraction (x) instead of site fraction (y), it is thus recommended to define the molar volume of a phase separately from its Gibbs energy if the phase is described by the CEF model. This can be realized through the user-defined molar volume property (Section User-Defined Property).
Using the Al-Ni binary system as an example, type “VARIABLE_X” is defined as property “Vm”:
Type_Definition v GES AMEND_PHASE_DESCRIPTION * VARIABLE_X Vm !
which means any phase with the Type_Definetion “v” will use mole fractions as the variables of Vm. Here are examples to define the molar volume parameters for the Liquid and L12_FCC phases:
Phase Liquid %v 1 1 !
Parameter Vm(Liquid,Al;0) 298.15 +V_Al_Liquid; 3000 N !
Parameter Vm(Liquid,Ni;0) 298.15 +V_Ni_liquid; 3000 N !
Phase L12_FCC %v 2 0.75 0.25 !
Parameter Vm(L12_FCC,Al;0) 298.15 +0.935*V_Al_fcc; 3000 N !
Parameter Vm(L12_FCC,Ni;0) 298.15 +0.935*V_Ni_fcc; 3000 N !
In this case, the molar volume of L12_FCC is calculated as:
|
|
(4) |
Although the L12_FCC phase is described by CEF model with two sublattices. Please refer to the User-defined Property in the example book for detail information.
Density
Density is calculated from molar volume and the molar weight. It requires the molar volume parameters in database. The unit for density is kg/m3. Density of a phase is defined as
|
|
(5) |
The density of a system with phase mixture is calculated from the molar weight and the molar volume of the mixture:
|
|
(6) |
Viscosity
A function to calculate viscosity of liquid phase is added into current Pandat™. The model used for describing the viscosity of liquid phase is semi-empirical relation presented in the paper by Seetharaman and Du [1994See],
|
|
(7) |
with
|
|
(8) |
where V is the molar volume of the melt, h the Plank’s constant, N the Avogadro’s number. ΔG* the Gibbs energy of activation, and can be calculated by
|
|
(9) |
where xi and xj are the molar fractions of component i and j, , Gibbs energy of activation of component i, and
, Gibbs energy of mixing. The calculation of molar volume is given in above sections. The parameter for the activation energy of a pure component in database TDB file has the format:
Parameter ActivationEnergy(Liquid,Al;0) 298.15 15051+13.519*T; 2000 N !
Surface Tension
Current Pandat™ has another new function to calculate surface tension of liquid phase. The model for calculating surface tension of liquid is the semi-empirical relationship proposed by Yeum et al. [1989Yeu] to estimate the surface tensions of binary alloys based on the model of Butler [1932But].
|
|
(10) |
where si, a'i and ai are the surface tension, activity at the surface and activity in the bulk of component i. And Si is the surface monolayer area,
|
|
(11) |
where b is geometric factor, N the Avogadro’s number, and Vi molar volume of component i. This approach was extended to calculate surface tensions of multicomponent liquid alloys [1997Zha]. The calculation of molar volume is the same as given in Section Volume. The ratio of the coordination number for the surface atoms to that for the atoms in the bulk phase, b, is represented by a parameter beta, described in database (.tdb) file in the format as
Parameter Beta(Liquid,Al;0) 298.15 0.83; 2000 N !